Volume of a Hemisphere: Easy Explanation, Formula, and Real-Life Examples

Have you ever looked at a bowl, an orange half, or even the top of an igloo and wondered what shape it is? That shape is called a hemisphere! It’s basically half of a sphere, like when you cut a ball right down the middle. And if you’ve ever been curious about how much space that half-sphere can hold inside it, you’re thinking about the volume of a hemisphere.

Learning how to find the volume of a hemisphere is super useful in real life. Engineers, designers, and even bakers use it all the time. From building domes to measuring scoops of ice cream, this simple concept appears more often than you might think.

In this article, we’ll explore what a hemisphere is, how to find its volume step by step, and some fun, real-life examples to make it all easy to understand. Don’t worry—it’s going to be simple, friendly, and fun to learn!

What Is a Hemisphere?

A hemisphere is exactly half of a sphere. If you imagine a basketball and slice it right through the middle, you’ll get two equal halves. Each half is a hemisphere. The word “hemi” means “half,” and “sphere” means a round ball-like shape. So, together, it means half a sphere.

You’ll find hemispheres everywhere. Our planet Earth, for example, is divided into two hemispheres—the Northern Hemisphere and the Southern Hemisphere. Even your favorite fruit, like an orange or melon, can become hemispheres when cut in half.

In geometry, when we talk about the volume of a hemisphere, we mean the amount of space it takes up inside. Just like how a bowl can hold soup, the hemisphere’s volume tells us how much it can contain.

Understanding the Volume of a Sphere

Before we find the volume of a hemisphere, we need to understand the volume of a sphere. A sphere is a perfectly round object, like a marble or planet. The formula for the volume of a sphere is: V=43πr3V = \frac{4}{3} \pi r^3V=34​πr3

Here:

• V is the volume,
• π (pi) is a special number (about 3.1416),
• r is the radius (the distance from the center to the surface).

This formula tells us how much space a full sphere occupies. Now, since a hemisphere is just half of a sphere, we can find its volume easily—by dividing the sphere’s volume by two!

Formula for the Volume of a Hemisphere

The formula for the volume of a hemisphere is simple: V=23πr3V = \frac{2}{3} \pi r^3V=32​πr3

That’s because a hemisphere is half of a sphere: Volume of hemisphere=12×43πr3=23πr3\text{Volume of hemisphere} = \frac{1}{2} \times \frac{4}{3} \pi r^3 = \frac{2}{3} \pi r^3Volume of hemisphere=21​×34​πr3=32​πr3

So, when you know the radius of your hemisphere, you can plug it into this formula to find its volume in cubic units. The answer tells you how much three-dimensional space it takes up.

Step-by-Step Example

Let’s take a simple example.

Suppose you have a hemisphere with a radius of 6 cm. We’ll find its volume step by step.

Step 1: Write down the formula: V=23πr3V = \frac{2}{3} \pi r^3V=32​πr3

Step 2: Plug in the radius: V=23π(6)3V = \frac{2}{3} \pi (6)^3V=32​π(6)3

Step 3: Simplify: V=23π(216)V = \frac{2}{3} \pi (216)V=32​π(216)

Step 4: Multiply: V=144πV = 144 \piV=144π

Step 5: Use π ≈ 3.1416 V≈144×3.1416=452.39V ≈ 144 \times 3.1416 = 452.39V≈144×3.1416=452.39

So, the volume of the hemisphere is about 452.39 cubic centimeters.

That’s it! Easy, right? This tells us that the hemisphere can hold around 452 cubic centimeters of space.

Units of Measurement

When we talk about the volume of a hemisphere, it’s important to use the right units. Volume is always measured in cubic units, because it deals with three dimensions—length, width, and height.

Here are some examples:

• If the radius is in centimeters (cm), the volume will be in cubic centimeters (cm³).
• If the radius is in meters (m), the volume will be in cubic meters (m³).
• For smaller shapes, like marbles, you might use millimeters (mm³).

Always remember to cube the unit, because you’re measuring space, not just distance.

Real-Life Examples of Hemispheres

The concept of a hemisphere isn’t just for math class—it’s all around us! Let’s look at some real-world examples where the volume of a hemisphere matters.

1. Bowls and Cups: Many bowls are shaped like half a sphere. Knowing the volume helps designers decide how much soup or cereal they can hold.
2. Domes and Buildings: Architects use the volume of hemispheres when designing domes for churches, mosques, and sports stadiums.
3. Ice Cream Scoops: The top of an ice cream scoop often looks like a hemisphere. Calculating the volume helps control portion sizes.
4. Water Tanks: Some storage tanks and measuring devices use hemispherical ends, and their volume needs to be known for capacity planning.

These examples show how geometry connects directly to daily life. When you know the formula, you can apply it to so many real-world objects!

How to Find the Radius if You Know the Volume

Sometimes you might know the volume of a hemisphere, but not the radius. You can find the radius by rearranging the formula.

The formula: V=23πr3V = \frac{2}{3} \pi r^3V=32​πr3

To find r, do this: r=3V2π3r = \sqrt[3]{\frac{3V}{2\pi}}r=32π3V​​

Let’s try a quick example.

If the volume of a hemisphere is 288π cm³, what’s the radius? r3=3×288π2π=8642=432r^3 = \frac{3 \times 288\pi}{2\pi} = \frac{864}{2} = 432r3=2π3×288π​=2864​=432 r=4323≈7.56r = \sqrt[3]{432} ≈ 7.56r=3432​≈7.56

So, the radius is about 7.56 cm.

Comparing Hemisphere Volume with Other Shapes

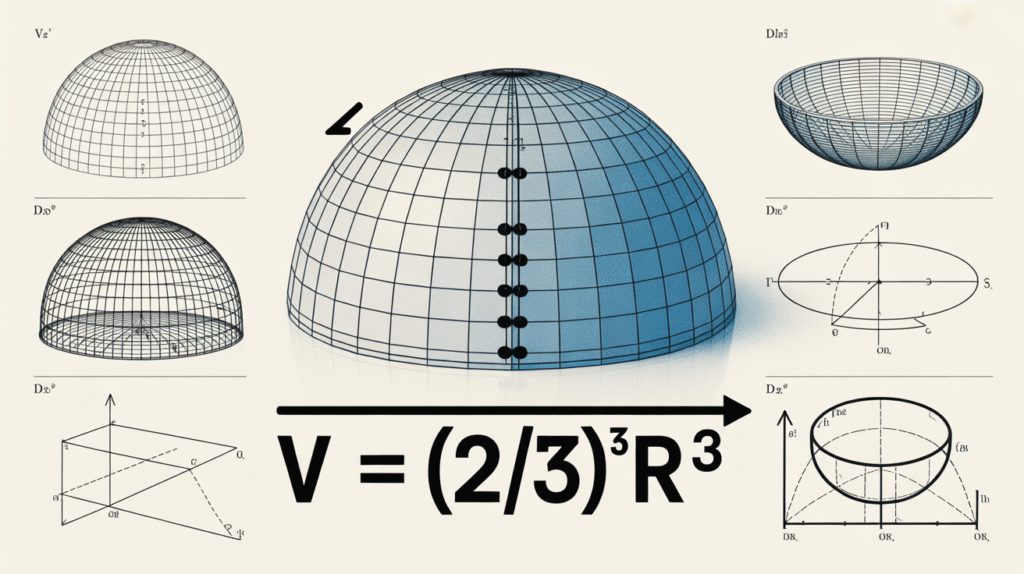
It’s fun to compare the volume of a hemisphere with other 3D shapes.

• A cube has a volume of a3a^3a3, where a is the side length.
• A cylinder has a volume of πr2h\pi r^2 hπr2h, where h is height.
• A cone has a volume of 13πr2h\frac{1}{3} \pi r^2 h31​πr2h.

What’s cool is that all these shapes use π or cube powers, just like the hemisphere. That’s because they all measure how much space is inside them. But the hemisphere’s curved shape makes its volume calculation unique and beautiful.

Why the Formula Works

You might be wondering why the volume of a hemisphere is exactly half the volume of a sphere. That’s because when you slice a sphere perfectly in half, each side keeps all the same properties—just in half the space.

This relationship was discovered long ago by ancient mathematicians, including Archimedes. He found that the volume of a sphere is two-thirds the volume of a cylinder with the same height and radius. So, naturally, a hemisphere is one-third of that cylinder’s volume. That’s where the fraction 23\frac{2}{3}32​ in our formula comes from!

Visualizing the Concept

Imagine filling a full ball with water. Then, pour that water into two equal half-bowls that match the ball’s shape. Each half-bowl holds exactly half the water from the full ball. That’s the easiest way to picture the volume of a hemisphere.

Visual thinking helps you remember the formula better. You can even try this at home using an orange or a small ball cut in half to see the shape in real life.

Common Mistakes to Avoid

When calculating the volume of a hemisphere, students sometimes make simple mistakes. Let’s fix those:

1. Forgetting to Cube the Radius: Remember, r3r^3r3 means multiply r by itself three times.
2. Mixing Up Area and Volume: Volume measures space inside; area measures surface covering.
3. Using the Wrong Units: Always cube your unit of measurement.
4. Leaving Out π: Don’t forget to include π—it’s what makes circular shapes accurate.

Checking your formula carefully will always save you from confusion!

Practical Uses in Science and Engineering

The volume of a hemisphere is important in many fields:

• Astronomy: Scientists calculate hemispherical shapes when studying planets or domes on observatories.
• Medicine: Doctors use hemisphere volumes to measure parts of organs or implants.
• Engineering: Engineers design hemispherical tanks, lenses, and even radar domes using this formula.

This shows that a simple geometry formula has real power and value beyond the classroom.

Fun Fact: Hemispheres in Nature

Nature loves hemispheres! Think of a turtle’s shell, a mushroom cap, or even a raindrop sitting on a surface. Many natural objects form hemispherical shapes because this shape is strong and efficient at holding volume. It spreads pressure evenly, which is why it’s used so often in architecture and design.

FAQs

1. What is the formula for the volume of a hemisphere?

The formula is V=23πr3V = \frac{2}{3} \pi r^3V=32​πr3, where r is the radius. It’s half the volume of a sphere.

2. What units do we use for volume?

Volume is always measured in cubic units, like cm³, m³, or mm³, depending on the radius’s unit.

3. How do you find the radius if you know the volume?

Use the reverse formula: r=3V2π3r = \sqrt[3]{\frac{3V}{2\pi}}r=32π3V​​

Plug in the volume and solve for r.

4. Why is π used in the formula?

π (pi) represents the circular nature of the shape. Since a hemisphere has a curved surface, π is needed in the calculation.

5. Can I find the volume using diameter instead of radius?

Yes! Since r=d2r = \frac{d}{2}r=2d​, the formula becomes: V=23π(d2)3V = \frac{2}{3} \pi \left(\frac{d}{2}\right)^3V=32​π(2d​)3

6. What’s the difference between hemisphere volume and surface area?

Volume measures the space inside the hemisphere, while surface area measures how much area the outside covers. They are related but not the same thing.

Conclusion

Now you know how easy it is to find the volume of a hemisphere! With just one simple formula—23πr3\frac{2}{3} \pi r^332​πr3—you can calculate how much space any half-sphere shape can hold. From ice cream scoops to domes and bowls, this concept shows up everywhere in our daily lives.

Remember, geometry isn’t just about numbers—it’s about understanding the world around us. When you see round shapes, you’ll now know how to think about their size in a whole new way.

So go ahead—grab a calculator, pick a shape, and explore the volume of a hemisphere yourself. You’ll be amazed at how math helps describe the beauty and balance of our three-dimensional world.